Содержание
Электродвигатель 3 кВт 1500 об/мин – АИР100S4 | АИР 100S4
АИР100S4 – трехфазный асинхронный электродвигатель 3 кВт 1500 об/мин с короткозамкнутым ротором. Общепромышленные двигатели типа АИР 100S4 и их аналоги с мощностью 3 кВт выпускаются несколькими производителями Украины, России, Китая и Беларуси. Имеют существенные отличия в уровне качества, но идентичные присоединительные и габаритные размеры, соответствующие ГОСТ 31606-2012. Питание – от сетей переменного тока 220 В или 380 В и частотой 50 Гц. Возможно подключение по схеме треугольник или звезда. Сила тока – 6,8 Ампер. Быстрая отправка по Украине в день заказа.
Цена
от 7260 грн
Хочу узнать больше о ценах
Технические характеристики двигателя АИР 100 S4
Таблица технических характеристик содержит эксплуатационные параметры двигателей 3 кВт 1500 об из паспорта электродвигателей АИР: мощность, напряжение, частоту вращения, номинальные токи, отношения моментов, пускового тока к номинальному и прочее.
| Характеристика электродвигателя | АИР100S4 |
| Мощность | 3 кВт |
| Частота вращения поля статора | 1500 об/мин |
| Скорость вращения вала | 1410 оборотов |
| Тип | Асинхронный |
| Напряжение питания | Трехфазное, 220/380 вольт |
| Монтажное исполнение | Лапы/фланец/комбинированное |
| Номинальный ток | 6,8 А |
| КПД | 82,6 % |
| Соотношение моментов тока Мп/Мн | 2,3 |
| Соотношение момента силы Mmax/Мн | 2,3 |
| Отношение тока Iп/Iн | 7,0 |
| Момент инерции | 0,01 кг∙м2 |
| Диаметр вала | 28 мм |
| Вес | 38,0 кг |
| Передний/задний подшипник | 6206 ZZ-C3 |
| Уровень шума | до 64 дБ |
Монтажные исполнения
В исполнении IM 2081 цена двигателя 3 кВт 1500 об/мин возрастает на 5%.
IM 1081 – исполнение на лапах
IM 2081 – комбинированное крепление
IM 3081 – фланцевый двигатель.
Параметры эл двигателей 3 кВт 1500 об/мин:
- Тип – общепромышленный трехфазный асинхронный;
- Режим работы – продолжительный S1;
- Термический класс изоляции обмоток F – до 150°С;
- Тип корпуса – чугун/силумин/алюминий;
- Степь защиты от влаги и пыли – IP54;
- Диаметр жилы обмоточного провода – 1,12 мм;
- Вес медной проводки – 2,96 кг;
Справочник обмоточных данных: размеры сердечника, количество пазов статора, шаг обмотки по пазам и тд.
Расшифровка обозначения АИР 100 S4 У2 IM 1081:
- АИР – тип электродвигателя
- 100 – условный габарит
- S – обозначение длины сердечника
- 4 – число пар полюсов
- У2 – категория размещения
- IM 1081 – монтажное исполнение лапы
Цены
Электродвигатели 3 кВт 1500 об/мин типа АИР 100S4 производятся в Украине, Беларуси, России и Китае.
| Электродвигатель 3 кВт 1500 об/мин | Цена, грн | ||
| Маркировка | Производитель | Без НДС | С НДС |
| АИР 100S4 | Беларусь | 8620 | 8620 |
| Украина | 8610 | 8610 | |
| Китай (низкое качество) | 7260 | 7260 | |
| Китай (высокое качество) | 8570 | 8570 | |
| 4А 100S4, 4АМ 100S4 | «Владимирский ВЭМЗ» с хранения | 6670 | 8000 |
| 4АМУ/АД/АДМ/4А | БУ | От 2333 | От 2800 |
В Украине двигатели АИР 100-ого габарита выпускают в Полтаве, Харькове и Ужгороде. Купить их также можно на нашем сайте. Новая Каховка НЕ производит АИР. Будьте внимательны при покупке и не переплачивайте мошенникам.
Различие в качестве
Основные параметры надежности электродвигателя 3 кВт 1500 об/мин:
- Толщина медного провода, масса меди – это устойчивость к перегрузкам. Разница количества меди может достигать 30%. Материалы обмотки дешевых электромоторов – алюмоцинк или медь с большим содержанием других металлов, как следствие – низкая нагревостойкость и несоответствие заявленной мощности.
- Подшипниковые щиты – массивность и качество металла в зоне посадочных мест под подшипник определяют устойчивость электромотора АИР 100 S4 к вибрациям, продольным и радиальным нагрузкам на вал. Возможна просадка посадочных мест и проворот подшипника, трещины и крошение крышек.
- Материал корпуса – чугунные массивные корпуса добротней алюминиевых, но тяжелей и легче крошатся – оба материала приемлемы. Дешевые электрические двигатели 3 кВт 1410 оборотов в минуту могут идти с некачественными корпусами с прессованного порошка втормета, это гораздо хуже!
- Подшипники – определяют виброшумовые показатели, стойкость к продольным нагрузкам, вибрации, ударам.
- Электрика и изоляция – низкое качество изоляции и пропитки обмотки в дешевых моторах, может привести к короткому или межвитковому замыканию. Также распространено оплавление изоляции выводных концов и замыкания в клеммной коробке низкокачественных двигателей.
Справочная информация
Чертеж и размеры АИР100S4
| Размеры вала | Крепеж по лапам | ||||||
| L3 | D4 | h3 | B1 | Н1 | В | D5 | L1 |
| 60 | 28 | 31 | 8 | 100 | 205 | 12 | 112 |
| Габариты корпуса | Крепеж по фланцу | |||||
| L | D | H | L2 | D1 | D2 | D3 |
| 385 | 215 | 270 | 63 | 250 | 215 | 180 |
- L3 – длина вала
- D4 – диаметр вала
- h3 – высота вала с шпонкой
- B1 – размер шпонки
- Н1 – высота до оси вала
- В – ширина по лапам
- D5 – диаметр отверстий на лапах
- L1 – по креплению лап
- L – длина мотора
- D – диаметр корпуса
- H – высота корпуса
- L2 – расстояние по креплениям
- D1 – диаметр фланца
- D2 – диаметр по отверстиям крепления
- D3 – диаметр торца фланца
Производители двигателей АИР100S4 3 кВт 1500 об/мин
Преимущественно в продаже на украинский рынок попадают электродвигатели АИР 3 кВт 1500 об/мин производства Китая (качественные и не очень), Белоруссии (Могилёвский завод «Электродвигатель», Полесьеэлектромаш), Украины (ХЭЛЗ, Электромотор), которые имеют одинаковое строение и конструктивные исполнения по ГОСТ 2479-79: АМУ100S4, 5АИ100S4, 5АМ100S4, АД100S4, А100S4.
| Производитель АИР 100 S4 | Рейтинг качества* | Характеристика двигателей 3 кВт 1500 об/мин |
| Дешевый Китай | ⭐⭐ | Подходят для стабильного напряжения, редких включений и плавных режимов работы (для привода вентиляторов и компрессоров). Малая масса меди, хрупкие корпуса и посадочные места, слабая изоляция. Не ремонтопригодны. |
| Качественный Китай | ⭐⭐⭐⭐ | Отличное соотношение цена-качество, долгий срок службы, сервис-фактор 1,1. Но и цена ближе к отечественным аналогам. |
| Украина | ⭐⭐⭐⭐(⭐) | Достойный уровень, сервис фактор 1.1, возможны детали Китайского производства. (только до 4 кВт) |
| Беларусь | ⭐⭐⭐⭐⭐ | Прекрасное качество, прочные подшипниковые щиты, надежный корпус, толстая медная обмотка и самая высокая цена |
*Субъективный рейтинг качества двигателей от независимых экспертов компании «Системы Качества»
Схемы подключения АИР 100 S4
Стандартные схемы подключения к сети трехфазного электродвигателя АИР 100S4:
- Звезда – для питания от промышленного напряжения 380 В, мотор работает с максимальным КПД;
- Треугольник – при работе от напряжения 220 В.
Подключение к бытовой сети, выполняется через пусковой и рабочий конденсаторы с потерей мощности 30%.
Модификации АИР 100S4
На базе стандартного АИР100S4 изготавливаются специализированные версии электродвигателей мощностью 3 кВт на 1500 оборотов:
- АИР100S4Е – с электромагнитным тормозом;
- АИР100S4Е2 – ЭМТ с растормаживающим устройством;
- АИРС100S4 – с повышенным скольжением;
- АИР100S4 Т2 – для влажного тропического климата;
- АИР100S4 ОМ2 – морское исполнение;
- АИР100S4 Х2 – химостойкая защита двигателя.
Где и как купить электродвигатель 3 кВт 1500 об/мин?
Безопасно и удобно покупайте электродвигатели АИР100S4 3 кВт 1500 об/мин производства Украины, Китая, России или Беларуси по ценам без наценок. Любые формы оплаты – по счету с НДС или без НДС, заказывайте отправку с наложенным платежом и оплачивайте только после осмотра. Забирайте двигатели самовывозом с нашего склада или на любимом перевозчике в своем городе: Новая Почта, САТ, Интайм, Деливери.
Для покупки двигателя АИР 100 S4 или бесплатной консультации – свяжитесь с менеджером!
Математическая модель асинхронного двигателя в мультифазной системе координат при несимметрии роторных цепей
- Электронный архив ТПУ
- Наука
- Периодические и продолжающиеся издания
- Известия ТПУ
Please use this identifier to cite or link to this item:
http://earchive.tpu.ru/handle/11683/68918
| Title: | Математическая модель асинхронного двигателя в мультифазной системе координат при несимметрии роторных цепей |
| Other Titles: | Modelling of induction motor in multiphase coordinate system for asymmetry rotor cage |
| Authors: | Глазырин, Александр Савельевич Полищук, Владимир Иосифович Тимошкин, Вадим Владимирович Баннов, Дмитрий Михайлович Исаев, Юсуп Ниязбекович Антяскин, Дмитрий Ильич Кладиев, Сергей Николаевич Филипас, Александр Александрович Ланграф, Сергей Владимирович Котин, Денис Алексеевич Ковалев, Владимир Захарович Glazyrin, Aleksandr Saveljevich Polishchuk, Vladimir Iosifovich Timoshkin, Vadim Vladimirovich Bannov, Dmitry Mikhailovich Isaev, Yusup Niyazbekovich Antyaskin, Dmitry Ilyich Kladiev, Sergey Nikolaevich Philipas, Alexander Alexandrovich Langraf, Sergey Vladimirovich Kotin, Denis Alekseevich Kovalev, Vladimir Zakharovich |
| Keywords: | асинхронные двигатели; математические модели; обрывы; роторы; диагностика; мультифазные системы; роторные цепи; повреждения; топливно-энергетический комплекс; георесурсы; дефекты; физические процессы; induction motor; mathematical model; squirrel-cage; broken rotor bar; technical condition |
| Issue Date: | 2021 |
| Publisher: | Томский политехнический университет |
| Citation: | Математическая модель асинхронного двигателя в мультифазной системе координат при несимметрии роторных цепей / А. С. Глазырин, В. И. Полищук, В. В. Тимошкин [и др.] // Известия Томского политехнического университета [Известия ТПУ]. Инжиниринг георесурсов. — 2021. — Т. 332, № 10. — [С. 213–227]. С. Глазырин, В. И. Полищук, В. В. Тимошкин [и др.] // Известия Томского политехнического университета [Известия ТПУ]. Инжиниринг георесурсов. — 2021. — Т. 332, № 10. — [С. 213–227]. |
| Abstract: | Актуальность исследования обусловлена острой необходимостью в теоретическом обосновании и практической разработке селективных методов диагностирования сложных внутренних повреждений мощных высоковольтных асинхронных двигателей с короткозамкнутым ротором, являющихся одним из главных элементов ответственных механизмов всех технологических процессов в топливно-энергетическом комплексе. Как правило, спецификой работы высоковольтных асинхронных двигателей с короткозамкнутым ротором в топливно-энергетическом комплексе как на стадии добычи и транспортировки георесурсов, так и на стадии их переработки являются тяжелые условия пуска, особенно это выражено для ответственных механизмов тепловых электростанций (питательные насосы, мельницы, дробилки, дымососы, дутьевые вентиляторы и т.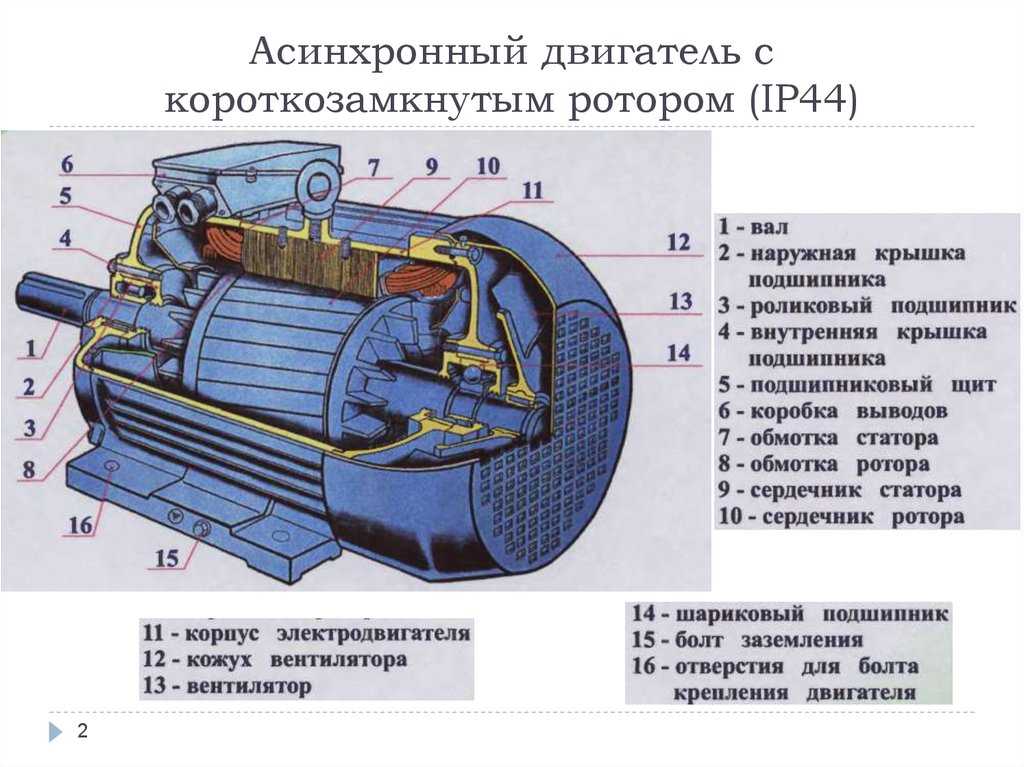 д.). Отказы асинхронных двигателей с короткозамкнутым ротором на тепловых электростанциях приводят либо к отключению энергоблока, либо как минимум к снижению уровня выработки электроэнергии. При этом, несмотря на тяжелейшие и, как правило, необратимые последствия от такого повреждения — дефекты в короткозамкнутой обмотке ротора асинхронных двигателей — защит от данного повреждения не существует, и выявляется оно только в период капитального ремонта. Обрыв стержня ротора, вызывающий несимметрию роторных цепей, в начальной стадии носит скрытый характер и является толчком для развития более опасных аварийных режимов. Отсутствие апробированных технических средств диагностики данного вида повреждения, прежде всего, связано с недостаточной формализацией математического описания процессов в асинхронных двигателях с короткозамкнутым ротором при возникновении дефектов в обмотке ротора. Объект: высоковольтные асинхронные электродвигатели переменного тока с короткозамкнутым ротором. Цель: разработать математическую модель асинхронной машины с несимметрией роторных цепей, адекватно отображающую физические процессы в машине при возникновении повреждений в обмотке ротора. д.). Отказы асинхронных двигателей с короткозамкнутым ротором на тепловых электростанциях приводят либо к отключению энергоблока, либо как минимум к снижению уровня выработки электроэнергии. При этом, несмотря на тяжелейшие и, как правило, необратимые последствия от такого повреждения — дефекты в короткозамкнутой обмотке ротора асинхронных двигателей — защит от данного повреждения не существует, и выявляется оно только в период капитального ремонта. Обрыв стержня ротора, вызывающий несимметрию роторных цепей, в начальной стадии носит скрытый характер и является толчком для развития более опасных аварийных режимов. Отсутствие апробированных технических средств диагностики данного вида повреждения, прежде всего, связано с недостаточной формализацией математического описания процессов в асинхронных двигателях с короткозамкнутым ротором при возникновении дефектов в обмотке ротора. Объект: высоковольтные асинхронные электродвигатели переменного тока с короткозамкнутым ротором. Цель: разработать математическую модель асинхронной машины с несимметрией роторных цепей, адекватно отображающую физические процессы в машине при возникновении повреждений в обмотке ротора. Методы и средства. Для достижения поставленной цели применялись теоретические методы исследований. К ним относятся: теория электрических машин, численные методы. Имитационное моделирование производилось в среде MatLab, а математическая обработка данных — в пакете MathCad. Результаты. Разработана n-фазная имитационная модель асинхронного двигателя, позволяющая исследовать обрыв стержня в беличьей клетке. Предложены аналитические выражения, которые описывают процессы в двигателе при неподвижном роторе. Методы и средства. Для достижения поставленной цели применялись теоретические методы исследований. К ним относятся: теория электрических машин, численные методы. Имитационное моделирование производилось в среде MatLab, а математическая обработка данных — в пакете MathCad. Результаты. Разработана n-фазная имитационная модель асинхронного двигателя, позволяющая исследовать обрыв стержня в беличьей клетке. Предложены аналитические выражения, которые описывают процессы в двигателе при неподвижном роторе.Relevance of the study is caused by an urgent need in theoretical justification and practical development of selective methods of diagnosing complex internal damages of powerful high-voltage squirrel-cage induction motors, which are one of the main elements of responsible mechanisms of all technological processes in fuel and energy complex. As a rule, specificity of work of high-voltage squirrel-cage motors in fuel and energy complex, both at a stage of extraction and transportation of georesources, and at a stage of their processing, are heavy conditions of start-up, especially it is expressed for critical mechanisms of thermal power plants (feed pumps, mills, crushers, smoke exhausters, blowers, etc.  ). Failures of squirrel-cage induction motors of critical mechanisms at thermal power plants lead to either shutdown of a power unit or at least to reduction of a level of electric power generation. At the same time, despite the gravest and, as a rule, irreversible consequences, there are no protections against such damage as defects in short-circuited winding of squirrel-cage induction motor rotor and such damage is detected only during overhaul. Broken-rotor-bar in the initial stage is latent and is a trigger for the development of more dangerous emergency modes. Lack of tested technical means for diagnostics of this type of damage is first of all related to insufficient formalization of mathematical description of processes in squirrel-cage induction motor when defects in rotor winding occur. Object: high voltage squirrel-cage induction AC motors. The aim of the research is to perform modeling of induction machine with electrical asymmetry rotor, adequately reflecting physical processes in the machine when damage occurs in the rotor cage. ). Failures of squirrel-cage induction motors of critical mechanisms at thermal power plants lead to either shutdown of a power unit or at least to reduction of a level of electric power generation. At the same time, despite the gravest and, as a rule, irreversible consequences, there are no protections against such damage as defects in short-circuited winding of squirrel-cage induction motor rotor and such damage is detected only during overhaul. Broken-rotor-bar in the initial stage is latent and is a trigger for the development of more dangerous emergency modes. Lack of tested technical means for diagnostics of this type of damage is first of all related to insufficient formalization of mathematical description of processes in squirrel-cage induction motor when defects in rotor winding occur. Object: high voltage squirrel-cage induction AC motors. The aim of the research is to perform modeling of induction machine with electrical asymmetry rotor, adequately reflecting physical processes in the machine when damage occurs in the rotor cage. Methods. Theoretical research methods were used to solve the problem. They include: the theory of electrical machines, numerical methods. Simulation modeling was performed in MatLab environment, and mathematical data processing in MathCad package. Results. An n-phase simulation model of an induction motor has been developed, which allows us to investigate the broken rotor bar in a squirrel-cage. Proposed analytical expressions, which describe the motor operation when the rotor is stationary. Methods. Theoretical research methods were used to solve the problem. They include: the theory of electrical machines, numerical methods. Simulation modeling was performed in MatLab environment, and mathematical data processing in MathCad package. Results. An n-phase simulation model of an induction motor has been developed, which allows us to investigate the broken rotor bar in a squirrel-cage. Proposed analytical expressions, which describe the motor operation when the rotor is stationary. |
| URI: | http://earchive.tpu.ru/handle/11683/68918 |
| ISSN: | 2413-1830 |
| Appears in Collections: | Известия ТПУ |
Show full item record
Google Scholar
Items in DSpace are protected by copyright, with all rights reserved, unless otherwise indicated.
Роман Упрощенная модель асинхронной машины с учетом частотной характеристики
На этой странице
АннотацияВведениеВыводыБлагодарностиСсылкиАвторское правоСтатьи по теме
Частотная характеристика электрооборудования должна учитываться при цифровом моделировании энергосистем.

1. Введение
Падение напряжения является обычным явлением при отказе энергосистемы, тогда как системная частота остается постоянной в крупных энергосистемах. Следовательно, традиционное моделирование и симуляция энергосистем сосредоточены на характеристиках напряжения силового оборудования с меньшим вниманием к частотной характеристике. Однако при высоком уровне распространения распределенной генерации [1, 2] частота системы будет колебаться, когда существует случайный дисбаланс между выработкой электроэнергии и спросом. Например, сбой или внезапное изменение нагрузки в микросети [3–5] вызовет относительно большое колебание частоты, поскольку инерция системы невелика.
Асинхронные машины, которые содержат асинхронные асинхронные двигатели и асинхронные генераторы, являются важным оборудованием в энергосистемах. Динамическая нагрузка включает в себя асинхронные двигатели [6–15] и большое количество ветрогенераторов, таких как асинхронные генераторы или асинхронные генераторы с двойным питанием (DFIG) [16–22]. Модель электромеханического переходного процесса третьего порядка для асинхронных машин широко используется при моделировании энергосистем. Традиционная форма этой модели не может представить частотную характеристику асинхронных машин, потому что эта упрощенная модель только предполагает, что частота постоянна, и игнорирует первую производную частоты при выводе. Результаты моделирования приемлемы при использовании традиционной переходной модели третьего порядка в условиях незначительных флуктуаций частоты или без учета флуктуаций частоты.
Для представления характеристик напряжения и частоты асинхронной машины во время моделирования в этой статье предлагается новая упрощенная переходная модель третьего порядка путем переопределения переменных и параметров традиционной модели.
2. Парковая модель асинхронной машины
На рис. 1 показаны схемы, применимые для анализа асинхронной машины. Цепи статора состоят из трехфазных обмоток , , и распределены в пространстве на 120° друг от друга. Цепи ротора содержат три распределенные обмотки , , и .
Пренебрегая насыщением, гистерезисом и вихревыми токами и предполагая чисто синусоидальное распределение волн потока, машинные уравнения можно записать следующим образом [25].
Уравнения напряжения статора и ротора задаются формулой
где представляет собой напряжение, представляет ток, представляет собой поток, связывающий обмотку, обозначенную нижним индексом, — сопротивление фазы статора, — сопротивление фазы ротора, а нижние индексы и — обмотки статора и ротора соответственно.
определяется как угол, на который ось фазной обмотки ротора опережает ось фазной обмотки статора в направлении вращения, при постоянной угловой скорости ротора:
и с постоянным проскальзыванием:
На рис. 2 видно, что электрическая угловая скорость системы отсчета и вращающейся системы отсчета составляет , ось обмотки ведет к оси обмотки в направлении вращения, а ось совпадает с осью фазной обмотки статора в начальный момент .
Применяя уравнение преобразования, получаем следующие выражения относительно преобразованных составляющих напряжения, потокосцеплений и токов [25].
Уравнения напряжения статора:
уравнения напряжения ротора:
Условия и напряжения трансформатора, аналогичные и .
Уравнения потокосцепления статора следующие:
Уравнения рассеяния магнитного потока ротора следующие:
где и , где , и – утечки статора, ротора и взаимные индуктивности соответственно.
Исключив фазное напряжение и ток в пересчете на составляющие, получим
Крутящий момент воздушного зазора получается путем деления мощности, передаваемой через воздушный зазор, на скорость вращения ротора в механических радианах в секунду:
где нижние индексы и обозначают ротор и статор соответственно.
3. Традиционная упрощенная модель асинхронной машины
За исключением переходных процессов статора,
Следующие переменные и параметры [25] определяются как
Переписывая (7), получаем
Напряжение ротора компонента (5) может быть записано как
Из приведенного выше уравнения можно записать как
Таким образом, (13) можно записать в виде
Аналогичным образом составляющая напряжения ротора определяется выражением
Этот термин обычно исключается при моделировании системы в предыдущих исследованиях, и уравнения модели переходного процесса асинхронной машины можно переписать следующим образом:
По сравнению с (15) и (16) и исключены из (17), что указывает на то, что частота рассматривается как константа в переходной модели третьего порядка асинхронной машины. Однако это предположение приведет к ошибкам, поскольку частота значительно изменится.
4. Новая упрощенная модель асинхронной машины
4.1. Переопределение переменных и параметров
Чтобы представить эффект колебания частоты и сохранить простоту переходной модели асинхронной машины третьего порядка, переменные и параметры должны быть переопределены следующим образом:
По сравнению с (11) и имеют линейную зависимость с потокосцеплением, посредством чего исключаются угловые частоты , и .
4.2. Уравнения напряжения ротора
Из (12) и (18) напряжение ротора компонента можно записать как
куда
Таким образом, (19) можно записать в виде
Исходя из аналогичного принципа, мы можем получить уравнение напряжения ротора компонента. Уравнения переходной модели асинхронной машины могут быть переписаны следующим образом:
не появляется в процессе вывода, что указывает на то, что частота не исключается в новой упрощенной переходной модели третьего порядка. С новым определением не учитываются угловая частота, индуктивность и параметры переходной модели, которые могут лучше отражать физические характеристики асинхронной машины в модели.
4.3. Уравнения напряжения статора
Чтобы сократить уравнения и сделать модель подходящей для программы устойчивости, мы исключаем токи ротора и выражаем взаимосвязь между током статора и напряжением относительно напряжения после переходного реактивного сопротивления. Таким образом, из (12) и (6) получаем
Подставив вышеприведенное уравнение вместо (4), уравнение напряжения статора компонента можно переписать как
Аналогичным образом можно получить составляющую уравнения напряжения статора, при этом уравнения напряжения статора можно записать в виде
Из (13) и (9) уравнение электромагнитного момента можно выразить как
4.

Уравнения переходной модели должны быть преобразованы в общедоступную систему отсчета при моделировании системы. На рис. 2 показано соотношение между системой отсчета и системой отсчета с аналогичной угловой скоростью в . угол, на который ось а ведет ось а в направлении вращения. Уравнение преобразования
В результате переходная модель получается следующим образом.
Уравнения переходного процесса:
уравнения напряжения статора:
уравнение электромагнитного момента:
уравнение ускорения ротора:
где на единицу и – начальное скольжение асинхронной машины. Если асинхронная машина потребляет мощность, то ; в противном случае, если асинхронная машина производит энергию.
5. Анализ модели
Известно, что асинхронные машины содержат асинхронные асинхронные двигатели и асинхронные генераторы; разница между ними заключается в уравнениях ускорения и напряжения ротора.
5.1. Асинхронный асинхронный двигатель Модель
Асинхронный двигатель — это обычная асинхронная машина, которая преобразует электрическую энергию в механическую на основе принципа электромагнитной индукции.
Уравнения переходного процесса:
уравнение ускорения:
уравнения напряжения статора:
5.2. Асинхронный генератор Модель
Асинхронные генераторы широко используются в ветроэнергетике. Большинство ранних ветряных генераторов представляют собой генераторы WT с фиксированной скоростью, а индукционный генератор работает с постоянной скоростью. Использование генераторов WT с переменной скоростью и постоянной частотой, таких как DFIG, является основным направлением в недавно построенных ветряных электростанциях. Однако модели различных индукционных генераторов схожи, что можно записать следующим образом.
Уравнения переходного процесса:
уравнение ускорения:
уравнения напряжения статора:
где и – эквивалентное напряжение ротора при следующих условиях: для генераторов ВТ с фиксированной скоростью – напряжение ротора, а для генераторов ВТ с переменной скоростью – постоянной частоты, которые могут подавать напряжение ротора через преобразователь на стороне ротора, – напряжение ротора .
6. Анализ моделирования
Упрощенная электросеть, содержащая составную нагрузку и ветрогенератор, как показано на рис. 3, построена в Matlab/Simulink для проверки производительности новой упрощенной модели асинхронной машины с учетом частотных характеристик. Таблицы 1 и 2 перечисляют параметры этой системы моделирования. Электросеть представляет собой изолированную энергосистему мощностью 300 кВт. Нагрузкой этой энергосистемы являются статическая нагрузка (ЗИП) и асинхронный асинхронный двигатель, потребляющие всю мощность, выдаваемую ветрогенератором при нормальной работе. Синхронный генератор используется в качестве преобразователя фазы для поддержания напряжения в системе. Для подачи реактивной мощности используются конденсаторы общей емкостью 75 кВАр.
Исследованы реакции новой упрощенной переходной модели третьего порядка асинхронной машины (как асинхронного двигателя, так и ветрогенератора) при уменьшении скорости ветра и отказе электрической нагрузки. Во время возмущения выходная мощность ветрогенератора колеблется, как и потребляемая мощность двигателя машины.
6.1. Случай A
В первом случае предполагается, что начальная нагрузка составляет 200 кВт, которая резко возрастает до 300 кВт примерно за 0,2 с, а затем возвращается к 200 кВт. На рис. 4 показано, что частота системы снижается в ответ на резкое увеличение нагрузки, а производная частоты показана на рис. 5. Впоследствии система достигает новой стабильной рабочей точки, и частота медленно восстанавливается после очевидных колебаний.
На рисунках 6, 7, 8 и 9 показано сравнение выходной активной и реактивной мощности традиционной упрощенной переходной модели третьего порядка, новой упрощенной переходной модели третьего порядка и подробной модели Парка асинхронного двигателя и ветрогенератора. По мере увеличения нагрузки ветрогенератор производит больше активной мощности и поглощает больше реактивной мощности. Показано, что выходная мощность новой упрощенной переходной модели третьего порядка с учетом частоты является более точной, чем у традиционной упрощенной переходной модели третьего порядка, и почти соответствует выходной мощности модели Парка.
В таблице 3 показаны накопленные ошибки между традиционной упрощенной переходной моделью третьего порядка и новой упрощенной переходной моделью третьего порядка по сравнению с подробной моделью (моделью Парка). Показано, что ошибка между новой упрощенной моделью переходного процесса с учетом частоты и детальной моделью меньше, чем между традиционной упрощенной моделью переходного процесса и детальной моделью.
6.2. Случай B
Возмущение скорости ветра используется для анализа влияния частоты во втором случае. Чтобы выделить колебания частоты в результате изменения скорости ветра, используются предполагаемые условия ветра с начальной скоростью ветра 10 м/с, которая падает до 7 м/с и восстанавливается до 10 м/с за 0,2 с, как показано на рис. Рисунок 10. На рисунке 14 показана выходная мощность генератора ВТ. На рисунке также показано, что генерируемая мощность ветра уменьшается в ответ на уменьшение скорости ветра, а активная мощность асинхронного двигателя компенсирует уменьшение при падении напряжения.
На рисунках с 12 по 15 показано сравнение выходной активной и реактивной мощности традиционной переходной модели третьего порядка, новой упрощенной переходной модели третьего порядка с учетом частоты и подробной модели Парка асинхронного двигателя и ветрогенератора. В новой упрощенной переходной модели третьего порядка с учетом частоты выходные данные асинхронного двигателя и ветрогенератора могут лучше отслеживать выходные данные подробной модели (модель Парка). Ошибка активной мощности меньше ошибки реактивной мощности (см. рис. 13 и 15).
Таблица 4 показывает, что накопленная ошибка активной мощности и реактивной мощности между новой упрощенной переходной моделью третьего порядка (как асинхронный двигатель, так и ветряной генератор) и моделью Парка меньше.
7.

В данной статье предлагается новая упрощенная переходная модель третьего порядка с учетом частотных характеристик асинхронной машины. Новая модель фокусируется на влиянии колебаний частоты на динамику энергосистемы. В новых определениях переменных напряжения за реактивным сопротивлением переопределяются как линейное уравнение потокосцепления. В результате уравнение напряжения ротора не связано с производными от частоты. Новая переходная модель применима для моделирования динамики энергосистемы со значительным изменением частоты. Результаты моделирования подтверждают, что новая упрощенная переходная модель третьего порядка эффективна и может более точно описывать динамику асинхронной машины по сравнению с традиционной упрощенной переходной моделью третьего порядка.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Благодарности
Эта работа поддерживается Национальным фондом естественных наук Китая (51137002), Фондами фундаментальных исследований для центральных университетов (10B101-08), Открытым фондом Ключевой лаборатории технологии оборудования для передачи и распределения энергии Цзянсу (2011JSSPD11).
Ссылки
-
С. А. Хапарде, «Инфраструктура для устойчивого развития с использованием технологий возобновляемых источников энергии в Индии», в Общем собрании IEEE Power Engineering Society (PES ’07) , июнь 2007 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
В. Эль-Хаттам, Т. С. Сидху и Р. Ситапати, «Оценка двух схем защиты от островков для радиальной распределительной системы, оснащенной ветряными турбинами с асинхронным генератором с самовозбуждением», IEEE Transactions on Energy Conversion , vol. 25, нет. 1, стр. 107–117, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
R.
H. Lasseter, «Microgrids», в IEEE Общество энергетического инженера Зимнее собрание , с. 305–308, январь 2002 г.
Посмотреть на:
Google Scholar
-
A. Dimeas и N. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. D. , «Эксплуатация мультиагентной системы для управления микросетями», IEEE Transactions on Power Systems , том. 20, нет. 3, стр. 1447–1455, 2005.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
Н. Хациаргириу, Х. Асано, Р. Иравани и К. Марней, «Микросети», IEEE Power and Energy Magazine , vol. 5, нет. 4, стр. 78–94, 2007 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
Р. Хе, Дж. Йе, Д. Линг и С. Панг, «Влияние параметров модели нагрузки на частоту системы во время переходных процессов в системе», Автоматизация электроэнергетических систем , вып.
34, нет. 24, pp. 27–30, 2010.
Просмотр по адресу:
Google Scholar
-
X. Zhang, P. Ju, Q. Chen et al., «Изучение и применение моделей нагрузки с учетом частотных характеристик», Журнал Университета Хохай (естественные науки) , том. 38, нет. 3, pp. 353–358, 2010.
Просмотр по адресу:
Google Scholar
-
R. He, J. Ye, H. Xu и B. Lang, «Моделирование нагрузки на основе измерений с учетом частотных характеристик, Труды Китайского электротехнического общества , том. 26, нет. 5, стр. 165–183, 2011.
Посмотреть по адресу:
Google Scholar
-
Ж.-К. Ван, Х.-Д. Чан, К.-Л. Чанг, А.-Х. Лю, К.-Х. Хуанг и С.-Ю. Хуанг, «Разработка частотно-зависимой модели составной нагрузки с использованием метода измерения», IEEE Transactions on Power Systems , vol.
9, нет. 3, стр. 1546–1556, 1994.
Посмотреть по адресу:
Сайт издателя | Академия Google
-
Л. Перейра, Д. Костерев, П. Макин, Д. Дэвис, Дж. Ундрилл и В. Чжу, «Временная динамическая модель асинхронного двигателя для исследований устойчивости в WSCC», IEEE Transactions on Power Systems , том. 17, нет. 4, стр. 1108–1115, 2002.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
К.-Х. Ценг, В.-С. Као и Ж.-Р. Лин, «Влияние модели нагрузки на настройки дистанционного реле», IEEE Transactions on Power Delivery , vol. 18, нет. 4, стр. 1140–1146, 2003.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
P. Ju, E. Handschin, ZN Wei и др., «Последовательная оценка параметров упрощенной модели асинхронного двигателя», IEEE Transactions on Power Systems , vol.
11, нет. 1, pp. 319–324, 1996.
Просмотр по адресу:
Google Scholar
-
Т. Омата и К. Уэмура, «Аспекты отклика напряжения нагрузки асинхронного двигателя», IEEE Transactions on Power Systems , об. 13, нет. 4, стр. 1337–1344, 1998.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
М. Джин, Х. Ренму и Д. Дж. Хилл, «Моделирование нагрузки путем поиска опорных векторов данных о нагрузке на основе полевых измерений», IEEE Transactions on Power Systems , vol. 21, нет. 2, стр. 726–735, 2006 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
Q. Ai, D. Gu и C. Chen, «Новые подходы к моделированию нагрузки, основанные на полевых испытаниях для расчетов устойчивости при быстрых переходных процессах», IEEE Transactions on Power Systems , vol.
21, нет. 4, стр. 1864–1873, 2006.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
Д. Л. Х. Айк, «Модель частотной характеристики системы общего порядка, включающая сброс нагрузки: аналитическое моделирование и приложения», IEEE Transactions on Power Systems , vol. 21, нет. 2, стр. 709–717, 2006 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
Г. В. Скотт, В. Ф. Вилрекер и Р. К. Шалтенс, «Взаимодействие генератора ветряных турбин с дизельными генераторами в изолированной энергосистеме», IEEE Transactions on Power Apparatus and Systems , vol. 103, нет. 5, pp. 933–937, 1984.
Просмотр по адресу:
Google Scholar
-
Дж. Г. Слоотвег, С. У. Х. Де Хаан, Х. Полиндер и В. Л. Клинг, «Общая модель для представления ветряных турбин с переменной скоростью в энергосистеме».
динамическое моделирование», IEEE Transactions on Power Systems , vol. 18, нет. 1, стр. 144–151, 2003 г.
Посмотреть по адресу:
Сайт издателя | Академия Google
-
C. Mi, M. Filippa, J. Shen и N. Natarajan, «Моделирование и управление синхронным генератором постоянной частоты с переменной скоростью и бесщеточным возбудителем», IEEE Transactions on Industry Applications , vol. 40, нет. 2, стр. 565–573, 2004 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
Дж. В. Тейлор, П. Э. МакШарри и Р. Буизза, «Прогнозирование плотности энергии ветра с использованием ансамблевых прогнозов и моделей временных рядов», IEEE Transactions on Energy Conversion , том. 24, нет. 3, стр. 775–782, 2009 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
З.
-С. Чжан, Ю.-З. Сун, Дж. Лин и Г.-Дж. Ли, «Координированное регулирование частоты ветряными электростанциями на основе асинхронных генераторов с двойным питанием», IET Renewable Power Generation , vol. 6, нет. 1, стр. 38–47, 2012 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
Ф. Ву, X.-П. Чжан, К. Годфри и П. Джу, «Анализ устойчивости малых сигналов и оптимальное управление ветровой турбиной с асинхронным генератором с двойным питанием», ИЭТ Генерация, передача и распределение , том. 1, нет. 5, стр. 751–760, 2007.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
Ф. Ву, X.-П. Чжан, П. Джу и М. Дж. Х. Стерлинг, «Децентрализованное нелинейное управление ветровой турбиной с асинхронным генератором с двойным питанием», IEEE Transactions on Power Systems , vol.
23, нет. 2, стр. 613–621, 2008 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
И. Д. Маргарис, С. А. Папатанасиу, Н. Д. Хациаргириу, А. Д. Хансен и П. Соренсен, «Управление частотой в автономных энергетических системах с высоким проникновением энергии ветра», IEEE Transactions on Sustainable Energy , vol. 3, нет. 2, стр. 189–199, 2012 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
П. Кундур, Power System Stability and Control , McGraw-Hill, New York, NY, USA, 1993.
Copyright
Copyright © 2014 Changalchun Cai et Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Моделирование и имитация асинхронного двигателя в системе координат αβ на базе Matlab
Главная Advanced Materials Research Advanced Materials Research Vols. 756-759 Моделирование и имитация асинхронного двигателя в…
Предварительный просмотр статьи
Аннотация:
Асинхронный двигатель имеет простую конструкцию, низкую стоимость, сравнимую с эффективностью управления двигателем постоянного тока при использовании технологии векторного управления. В этой статье основное внимание уделяется трехфазному асинхронному двигателю, на долю которого приходится большая часть машин переменного тока. Во-первых, в этой статье строится система векторного управления асинхронным двигателем, затем выводятся математические модели асинхронного двигателя на основе системы координат. Наконец, в статье строится имитационная модель асинхронного двигателя на основе системы координат в Matlab/Simulink, приводятся и анализируются результаты моделирования.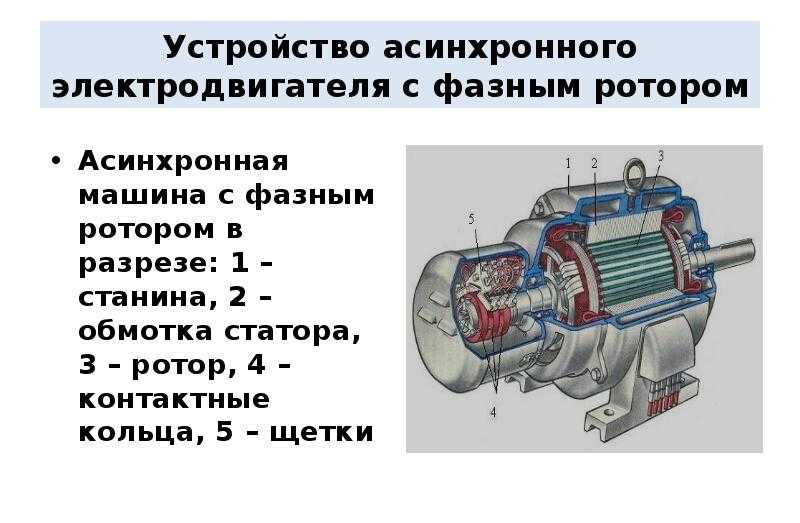
Доступ через ваше учреждение
использованная литература
[1]
Ху Чун Юэ. Современная технология регулирования скорости переменного тока[M]. Пекин: Machinery Industry Press, 2001 (на китайском языке).
[2]
Чен Боши.
[3]
Малиновски М., Гопакумар К., Родригес Дж. и др. Обзор каскадных многоуровневых инверторов[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 219.7−2206.
DOI: 10.1109/tie.2009.2030767
[4]
REN Yi-feng, LIU Gang, ZHAO Min. Применение активного управления подавлением возмущений в прямом управлении крутящим моментом асинхронного двигателя [J]. Электропривод, 2009, 39(6): 15−18.
[5]
Тэ-Хьюнг Ким, Бьюнг-Кук Ли, Эхсани, М.
DOI: 10.1109/apec.2003.1179231
[6]
Депенброк М. Прямой самоконтроль (DSC) асинхронных машин с инверторным питанием [J]. IEEE транс. ЧП, 1988, 3(4): 420-429.
DOI: 10.1109/63.17963
[7]
Ду Юнхун, Ли Чжэфэн, Лю Чжиган. Двойная замкнутая система асинхронных двигателей с непрямой ориентацией поля [J].

 Подключение к бытовой сети, выполняется через пусковой и рабочий конденсаторы с потерей мощности 30%.
Подключение к бытовой сети, выполняется через пусковой и рабочий конденсаторы с потерей мощности 30%. H. Lasseter, «Microgrids», в IEEE Общество энергетического инженера Зимнее собрание , с. 305–308, январь 2002 г.
H. Lasseter, «Microgrids», в IEEE Общество энергетического инженера Зимнее собрание , с. 305–308, январь 2002 г.  34, нет. 24, pp. 27–30, 2010.
34, нет. 24, pp. 27–30, 2010. 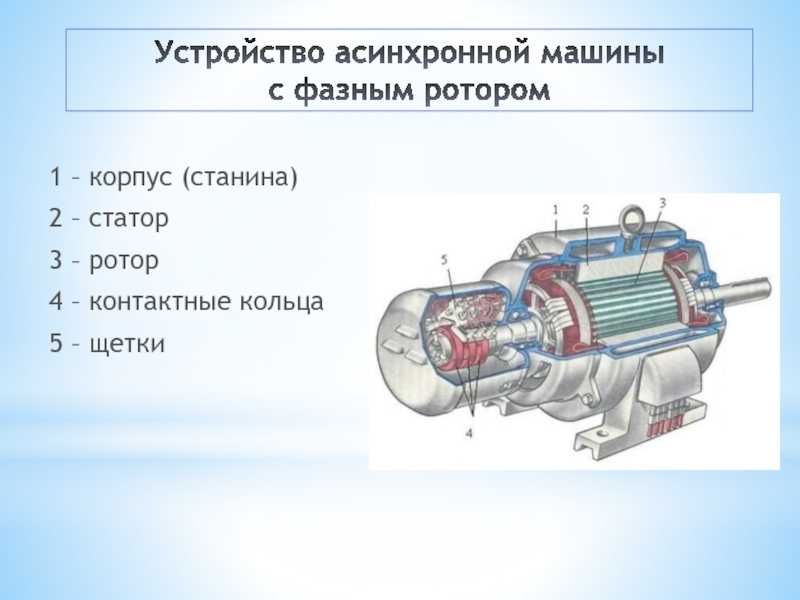 9, нет. 3, стр. 1546–1556, 1994.
9, нет. 3, стр. 1546–1556, 1994.  11, нет. 1, pp. 319–324, 1996.
11, нет. 1, pp. 319–324, 1996.  21, нет. 4, стр. 1864–1873, 2006.
21, нет. 4, стр. 1864–1873, 2006.  динамическое моделирование», IEEE Transactions on Power Systems , vol. 18, нет. 1, стр. 144–151, 2003 г.
динамическое моделирование», IEEE Transactions on Power Systems , vol. 18, нет. 1, стр. 144–151, 2003 г.  -С. Чжан, Ю.-З. Сун, Дж. Лин и Г.-Дж. Ли, «Координированное регулирование частоты ветряными электростанциями на основе асинхронных генераторов с двойным питанием», IET Renewable Power Generation , vol. 6, нет. 1, стр. 38–47, 2012 г.
-С. Чжан, Ю.-З. Сун, Дж. Лин и Г.-Дж. Ли, «Координированное регулирование частоты ветряными электростанциями на основе асинхронных генераторов с двойным питанием», IET Renewable Power Generation , vol. 6, нет. 1, стр. 38–47, 2012 г.  23, нет. 2, стр. 613–621, 2008 г.
23, нет. 2, стр. 613–621, 2008 г. 